[게임서버] 삼각함수, 역 삼각 함수

삼각함수와 역삼각 함수의 가장 기초적인 부분 부터 이해하고 시작을 해야겠다!

삼각함수를 배우기 전에 우리는 삼각비를 배우고 시작해야한다.

- 삼각비란?

 

삼각비는 직각삼각형에서 두 변의 길이의 비를 나타낸 것입니다

닮음인 직각삼각형끼리는 각 변의 길이의 비가 모두 같을 것입니다.

다음은 각각의 삼각형의 각 변의 길이를 일정한 간격으로 늘린 것입니다.

삼각 비는 각각의 변들의 길이의 비를 나타낸 것을 삼각 비라고 합니다.

그중 델타 각을 기준으로 

다음과 같이 삼각비를 구할 수 있습니다. 이것이 삼각비의 대한 기본 공식이고 sin, cos, tan 라는 삼각비가 여기서 나오게 됩니다.

- 삼각함수란?

이제 이러한 삼각비를 이용해서 삼각함수를 사용하는 것은 어렵지 않습니다.

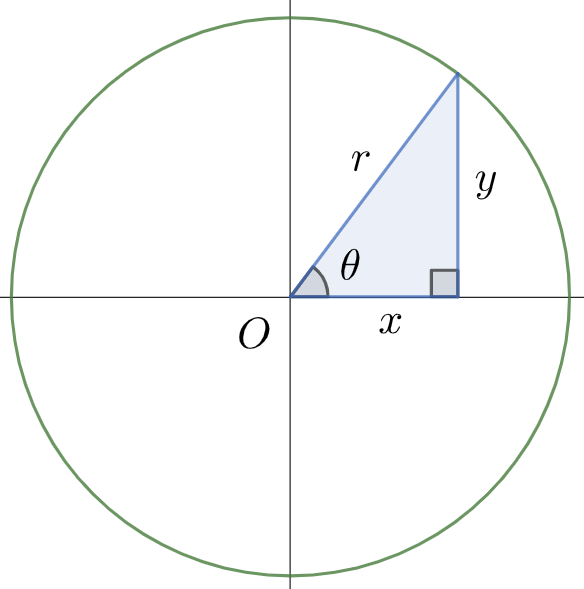
다음과 같은 r을 빗면으로 사용하면서 r을 반지름으로 하는 원과 삼각형이 있습니다.

그래서 이제 이 델타각을 이용하여서 우리는 삼각형의 r , x, y 를 구할 수 있습니다.

예를들어 여기서 만약 빗면 r 이 1이라고 한다면 x , y 는 x/ r , y/ r 인 cos, sin 이되어서 x , y 를  cos, sin에 대입할 수 있다는 개념이 삼각함수의 기본이라고 생각하면 됩니다.

- 역함수

역 함수는 간단하게 y = x + 1이라는 함수가 있다면 여기에 x에 1을 넣었을 때 y가 2가나온다는 것을 아는 것은 일반 함수이다. 하지만 반대로 y가 2가 나오기 위해선 x가 무엇이여야하는가에 대한 질문에 답을 구하는 방법은 x에 1이란 숫자를 직접 대입하게 끔 하는 x = y - 1 의 함수를 직접 제작하는 경우를 우리는 역함수라고한다.

- 역 삼각 함수

역 삼각함수는 간단하게 역함수처럼 이번에는 sin, cos, tan가 주어졌을 때 델타 각을 구하는 것이 목적이다.  

(1). 역사인함수 (arcsin x)

sin:[− 𝜋 /2, 𝜋 /2]→[−1,1]sin:[−𝜋/2,𝜋/2]→[−1,1] 일대일 대응

⇒⇒ sin−1:[−1,1]→[− 𝜋 /2, 𝜋 /2]sin−1:[−1,1]→[−𝜋/2,𝜋/2] 역사인 함수

⇒⇒ y=sin−1x𝑦=sin−1⁡𝑥

sin 함수에서 조건에 부합하는 일대일 대응이 되는 부분

sin(sin−1(x))=x,x∈[−1,1],sin−1(sin(x))=x,x∈[− 𝜋 /2, 𝜋 /2] 정의역 과 치역을 구할 수 있다.

(2). 역코사인 함수 (arccos x)

cos:[0,π]→[−1,1]cos:[0,𝜋]→[−1,1] 일대일 대응

⇒⇒ cos−1:[−1,1]→[0,π]cos−1:[−1,1]→[0,𝜋] 역코사인 함수

⇒⇒ y=cos−1x𝑦=cos−1⁡𝑥

cos 함수에서 조건에 부합하는 일대일 대응이 되는 부분

cos(cos−1(x))=x,x∈[−1,1],cos−1(cos(x))=x,x∈[0,π]cos⁡(cos−1⁡(𝑥))=𝑥,𝑥∈[−1,1],cos−1⁡(cos⁡(𝑥))=𝑥,𝑥∈[0,𝜋]

**역코사인 함수의 치역은 양수이다. 즉, 역코사인의 값은 음수가 없다는 사실을 기억하자.

(3). 역탄젠트 함수 (arctan x)

tan:(− 𝜋 /2, 𝜋 /2)→(−∞,∞)tan:(−𝜋/2,𝜋/2)→(−∞,∞) 일대일 대응

⇒⇒ tan−1:(−∞,∞)→(− 𝜋 /2, 𝜋 /2)tan−1:(−∞,∞)→(−𝜋/2,𝜋/2) 역탄젠트 함수

⇒⇒ y=tan−1x𝑦=tan−1⁡𝑥

*()() 는 열린구간을 의미한다. 점근선에 해당하는 값은 포함되지 않는다.

tan 함수에서 조건에 부합하는 일대일 대응이 되는 부분

tan−1(0)=0,tan−1(1)= 𝜋 /4tan−1⁡(0)=0,tan−1⁡(1)=𝜋/4

역탄젠트에서는 위의 두 식을 가장 많이 사용한다. 역탄젠트에서는 역사인, 역코사인 처럼 대수적인 계산을 하는 문제가 나오지 않는다. 역탄젠트 x𝑥의 그래프의 개형을 알고 있는 것이 중요하다.